Beautiful plots while simulating loss in two-part Procrustes problem

Today, I was working on a two part Procrustes problem and wanted to find out why my minimization algorithm sometimes does not converge properly or renders unexpected results. The loss function to be minimized is

\[ L(\mathbf{Q},c) = \| c \mathbf{A_1Q} - \mathbf{B_1} \|^2 + \| \mathbf{A_2Q} - \mathbf{B_2} \|^2 \rightarrow min \]

with \(\| \cdot \|\) denoting the Frobenius norm, \(c\) is an unknown scalar and \(\mathbf{Q}\) an unknown rotation matrix, i.e. \(\mathbf{Q}^T\mathbf{Q}=\mathbf{I}\). \(\;\mathbf{A_1}, \mathbf{A_2}, \mathbf{B_1}\), and \(\mathbf{B_1}\) are four real valued matrices. The minimum for \(c\) is easily found by partial derivation and setting to zero.

\[ c = \frac {tr \; \mathbf{Q}^T \mathbf{A_1}^T \mathbf{B_1}} { \| \mathbf{A_1} \|^2 } \]

By plugging \(c\) into the loss function \(L(\mathbf{Q},c)\) we get a new loss function \(L(\mathbf{Q})\) that only depends on \(\mathbf{Q}\). This is the starting situation.

When trying to find out why the algorithm to minimize \(L(\mathbf{Q})\) did not work as expected, I got stuck. So I decided to conduct a small simulation and generate random rotation matrices to study the relation between the parameter \(c\) and the value of the loss function \(L(\mathbf{Q})\). Before looking at the results, let’s visualize the results for the first part of the above Procrustes problem, with \(c\) having the same solution as before.

\[ L(\mathbf{Q},c) = \| c \mathbf{A_1Q} - \mathbf{B_1} \|^2 \rightarrow min \]

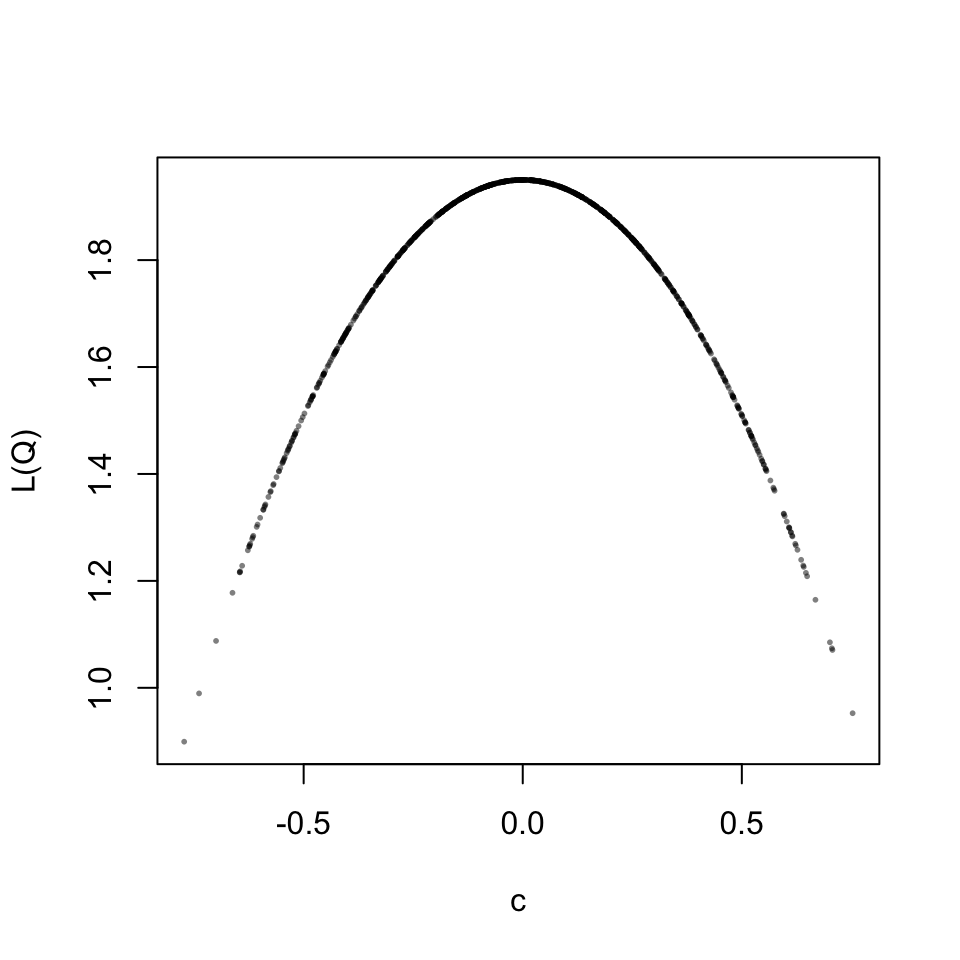
This is a well behaved relation, for each scaling parameter the loss value is identical. Now let’s look at the full two-part loss function. The result turns out to be beautiful.

For the graphic above I used the following matrices.

\[ A1= \begin{pmatrix} 0.0 & 0.4 & -0.5 \\ -0.4 & -0.8 & -0.5 \\ -0.1 & -0.5 & 0.2 \\ \end{pmatrix} \mkern18mu , \mkern36mu B1= \begin{pmatrix} -0.1 & -0.8 & -0.1 \\ 0.3 & 0.2 & -0.9 \\ 0.1 & -0.3 & -0.5 \\ \end{pmatrix} \] \[ A2= \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \\ \end{pmatrix} \mkern18mu , \mkern36mu B2= \begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} \]

And the following R-code.

tr <- function(X) sum(diag(X))

# random matrix type 1
rmat_1 <- function(n=3, p=3, min=-1, max=1){
  matrix(runif(n*p, min, max), ncol=p)
}

# random matrix type 2, sparse
rmat_2 <- function(p=3) {
  diag(p)[, sample(1:p, p)]
}

# generate random rotation matrix Q. Based on Q find 
# optimal scaling factor c and calculate loss function value
#
one_sample <- function(n=2, p=2)
{
  Q <- mixAK::rRotationMatrix(n=1, dim=p) %*%         # random rotation matrix
    diag(sample(c(-1,1), p, rep=T))                   # additionally 
  s <- tr( t(Q) %*% t(A1) %*% B1 ) / norm(A1, "F")^2  # scaling factor c
  rss <- norm(s*A1 %*% Q - B1, "F")^2 + 
         norm(A2 %*% Q - B2, "F")^2 
  c(s=s, rss=rss)
}

# find c and rss or many random rotation matrices
#
set.seed(10)  # nice case for 3 x 3
n <- 3
p <- 3
A1 <- round(rmat_1(n, p), 1)
B1 <- round(rmat_1(n, p), 1)
A2 <- rmat_2(p)
B2 <- rmat_2(p)

x <- rdply(40000, one_sample(3,3)) 
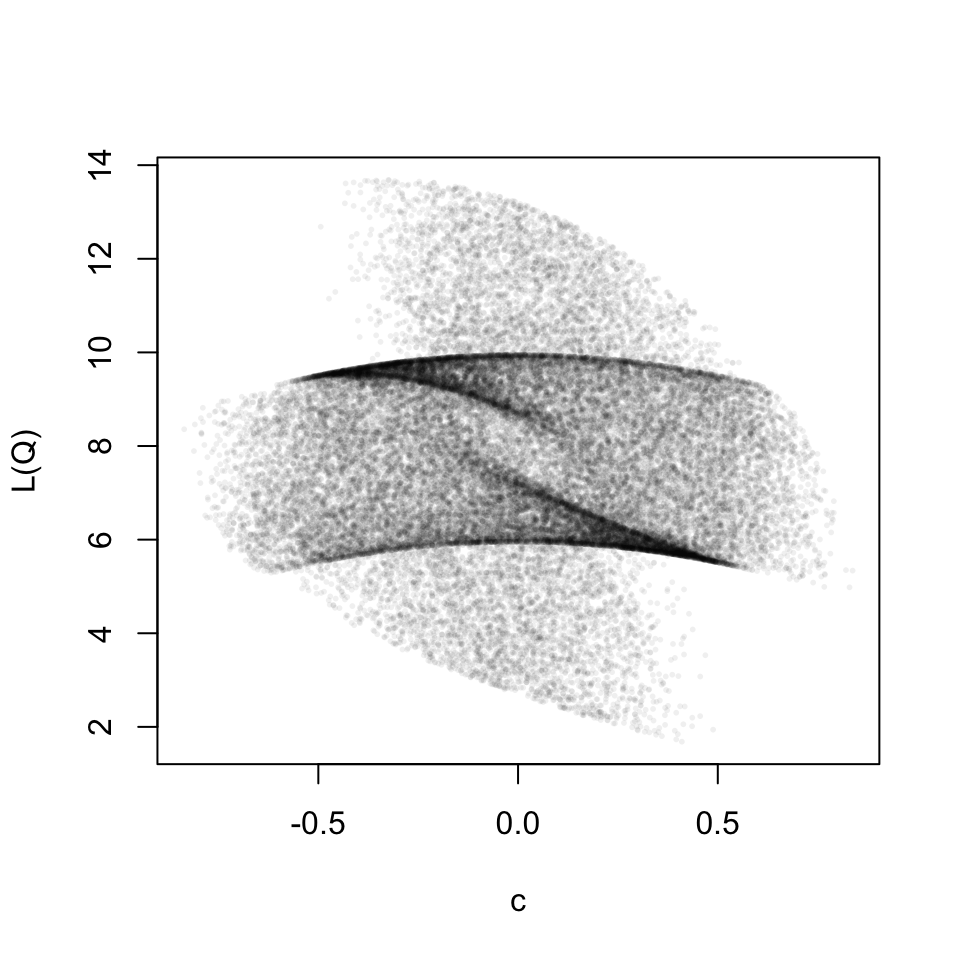
plot(x$s, x$rss, pch=16, cex=.4, xlab="c", ylab="L(Q)", col="#00000010")

Below you find some more graphics with different matrices as inputs.

Here, we do not have a one-to-one relation between the scaling parameter and the loss function any more. I do not quite know what to make of this yet. But for now I am happy that it has aesthetic value.