Thurstone Skalierung

psychometrics

statistics

Eine Einführung in die Thurstone Skalierung.

Published

January 29, 2013

Methode des paarweisen Vergleichs (Law of Comparative Judgement [LCJ])

Eine gute Einführung in die Thurstone-Skalierung bietet Gerich (2010). Die genutzten Beispiele enstammen diesem Buchkapitel.

Zwei Objekte $i$ und $j$ werden beurteilt. Der Urteiler urteilt nicht jedes Mal exakt. Die Urteile variieren um die wahren Skalenwerte $s_{i}$ und $s_{j}$ .

In dem Bild gilt die Beziehung $s_{i} > s_{j}$ . Das Objekt $i$ hat auf der Urteilsdimension einen geringeren wahren Wert als das Objekt $j$ . Die Beurteilung des Objektes enthält jedoch ein zufällige Fehlerkomponente. Die realen $i$ und $j$ Werte schwanken normalverteilt um den die wahren Werte $s_{i}$ und $s_{j}$ . Wie wahrscheinlich ist es nun, dass sich bei der Beurteilung, bedingt durch den zufälligen Fehler, die Reihenfolge der Objekte auf der Dimension umkehrt? Hierzu wird die Verteilung der Differenzen der Urteile betrachtet. Die Differenz sei $d = s_{i} > s_{j}$ . Die Verteilung der Differenzen ist nachfolgend dargestellt.

Der Erwartungswert (die wahre Differenz zwischen den Objekten) entspricht $s_{i} - s_{j} =$ -1.5. Die Streuung der Differenzen ist: $σ_{i j} = \sqrt{σ_{i}^{2} + σ_{j}^{2} - 2 r_{i j} σ_{i} σ_{j}}$ .

Standardisierung der Differenzen: $z_{i j} = \frac{0 - (s_{i} - s_{j})}{σ_{i j}} = \frac{s_{j} - s_{i}}{σ_{i j}}$ .

Annahmen:

Die Urteile streuen bei jedem Objekt im gleichen Ausmaß um den wahren Wert, d.h. die Streuungen sind identisch: $σ_{i}^{2} = σ_{j}^{2}$
Die Korrelation der Urteile zwischen den Objekten ist konstant: $r_{i j} = r_{i k}$

Unter Einbeziehung der Annahmen vereinfacht sich die Streuung der Urteilsdifferenzen zu $z_{i j} = \frac{s_{j} - s_{i}}{σ^{2} + σ^{2} - 2 r σ^{2}} = \frac{s_{j} - s_{i}}{2 σ^{2} (1 - r)}$ .

Es zeigt sich, dass der Nenner für alle Paarvergleiche einen konstanten Wert annimmt. D.h. es handelt sich stetS um die gleiche konstante lineare Transformation für jeden Paarvergleich. Aus diesem Grund kann der Nenner ohne Informationsverlust durch einen beliebigen anderen konstanten Wert ersetzt werden, z.B. den Wert $1$ . Zwar ändert sich hierbei der absolute Wert, nicht jedoch die Relationen der Werte. Diese von Thurstone eingeführte Vereinfachung wird als CASE V bezeichnet. In Folge vereinfacht sich die Differenz der Urteile zu $z i j = s_{j} - s_{i}$

Vorgehensweise

Gegeben sei folgende Auszählung an der Dominanzurteile. Das Spaltenmerkmal dominiert das Zeilenmerkmal.

        Alkohol Ecstasy Hanf Heroin Kokain Nikotin Kaffee
Alkohol      50       7   76      0     10      79    100
Ecstasy      93      50  100     21     65      97     97
Hanf         24       0   50      3      3      41     93
Heroin      100      79   97     50     93     100    100
Kokain       90      35   97      7     50      93    100
Nikotin      21       3   59      0      7      50     97
Kaffee        0       3    7      0      0       3     50

Es werden nun für jeden Vergleich die relative Häufigkeit für das Auftreten des Dominanzurteils berechnet.

        Alkohol Ecstasy Hanf Heroin Kokain Nikotin Kaffee
Alkohol    0.50    0.07 0.76   0.00   0.10    0.79   1.00
Ecstasy    0.93    0.50 1.00   0.21   0.65    0.97   0.97
Hanf       0.24    0.00 0.50   0.03   0.03    0.41   0.93
Heroin     1.00    0.79 0.97   0.50   0.93    1.00   1.00
Kokain     0.90    0.35 0.97   0.07   0.50    0.93   1.00
Nikotin    0.21    0.03 0.59   0.00   0.07    0.50   0.97
Kaffee     0.00    0.03 0.07   0.00   0.00    0.03   0.50

Die relativen Häufigkeiten werden nun in die zugehörigen z-Werte umgewandelt. Die P-Werte $0$ und $1$ Werte haben als korrespondierende z-Werte -/+ Inf. Aus diesem Grund werden diese Werte hier mit $.01$ bzw. $.99$ substituiert, um nutzbare z-Werte zu erhalten.

        Alkohol Ecstasy  Hanf Heroin Kokain Nikotin Kaffee
Alkohol    0.00   -1.48  0.71  -2.33  -1.28    0.81   2.33
Ecstasy    1.48    0.00  2.33  -0.81   0.39    1.88   1.88
Hanf      -0.71   -2.33  0.00  -1.88  -1.88   -0.23   1.48
Heroin     2.33    0.81  1.88   0.00   1.48    2.33   2.33
Kokain     1.28   -0.39  1.88  -1.48   0.00    1.48   2.33
Nikotin   -0.81   -1.88  0.23  -2.33  -1.48    0.00   1.88
Kaffee    -2.33   -1.88 -1.48  -2.33  -2.33   -1.88   0.00

Die z-Werte werden nun zeilenweise gemittelt (Spalte z.mean). Anschließend wird der Nullpunkt der Skala auf den kleinsten Wert gesetzt, d.h. der kleinste Wert wird abgezogen (Spalte s.i). Diese Werte bilden die $s_{i}$ , d.h. die Werte der Objekte auf dem Beurteilungskontinuum.

        z.mean  s.i
Alkohol  -0.18 1.57
Ecstasy   1.02 2.77
Hanf     -0.79 0.95
Heroin    1.59 3.34
Kokain    0.73 2.47
Nikotin  -0.63 1.12
Kaffee   -1.75 0.00

Kaffee wird als am ungefährlichsten, Heroin als am gefährlichsten eingestuft. Der Unterschied zwischen Kaffee und Alkohol (1.57) entspricht in etwa dem von Alkohol und Heroin (1.77).

Rekonstruktion der P-Werte

Im Folgenden werden die P-Werte aus den Skalenwerten rekonstruiert. Dies dient dazu, die Güte der Reproduktion zu beurteilen.

Für jedes Stimuluspaar wird die Differenz der $s_{i}$ Werte berechnet. Dies entspricht den rekonstruierten z-Werten $z^{'}$ .

        Alkohol Ecstasy  Hanf Heroin Kokain Nikotin Kaffee
Alkohol    0.00   -1.20  0.61  -1.77  -0.91    0.45   1.57
Ecstasy    1.20    0.00  1.81  -0.57   0.29    1.65   2.77
Hanf      -0.61   -1.81  0.00  -2.38  -1.52   -0.17   0.95
Heroin     1.77    0.57  2.38   0.00   0.86    2.22   3.34
Kokain     0.91   -0.29  1.52  -0.86   0.00    1.35   2.47
Nikotin   -0.45   -1.65  0.17  -2.22  -1.35    0.00   1.12
Kaffee    -1.57   -2.77 -0.95  -3.34  -2.47   -1.12   0.00

Die z-Werte stellen die Quartile der Normalverteilung dar. Die zugehörigen Wahrscheinlichkeiten können aus der NV-Tabelle abgelesen werden.

        Alkohol Ecstasy Hanf Heroin Kokain Nikotin Kaffee
Alkohol    0.50    0.12 0.73   0.04   0.18    0.67   0.94
Ecstasy    0.88    0.50 0.97   0.28   0.61    0.95   1.00
Hanf       0.27    0.03 0.50   0.01   0.06    0.43   0.83
Heroin     0.96    0.72 0.99   0.50   0.81    0.99   1.00
Kokain     0.82    0.39 0.94   0.19   0.50    0.91   0.99
Nikotin    0.33    0.05 0.57   0.01   0.09    0.50   0.87
Kaffee     0.06    0.00 0.17   0.00   0.01    0.13   0.50

Um die Güte der Reprduktion zu beurteilen, wird elementweise die absolute Differenz zwischen der beiden P-Matrizen gebildet.

        Alkohol Ecstasy Hanf Heroin Kokain Nikotin Kaffee
Alkohol    0.00    0.05 0.03   0.04   0.08    0.12   0.06
Ecstasy    0.05    0.00 0.03   0.07   0.04    0.02   0.03
Hanf       0.03    0.03 0.00   0.02   0.03    0.02   0.10
Heroin     0.04    0.07 0.02   0.00   0.12    0.01   0.00
Kokain     0.08    0.04 0.03   0.12   0.00    0.02   0.01
Nikotin    0.12    0.02 0.02   0.01   0.02    0.00   0.10
Kaffee     0.06    0.03 0.10   0.00   0.01    0.10   0.00

Der durchschnittliche absolute Differenz wird als Indikator für die Güte des Modells genutzt. Der Wert sollte unter $.03$ liegen.

[1] 0.05

Das Modell weist somit eine mittelmäßige Anpassung auf.

Methode der sukzessiven Intervalle (Method of Succesive Intervals [MIS])

Theorie

Ziel: Information über den Abstand der Objekte (intervallskaliert)

Annahmen: (Thurstone, 1927) * Urteiler kann Merkmalskontinuum in Kategorien aufteilen. * Kategoriengrenzen schwanken um wahren Wert. * Wahrscheinlichkeit für Realisierung einer Kategoriengrenze ist normalverteilt. * Beurteilung einer Merkmalsausprägung schwankt ebenfalls zufällig. * Wahrscheinlichkeit für Realisierung eines Urteils auch normalverteilt. * Urteiler stuft Reiz unterhalb Kategoriengrenze ein, wenn die im Urteil realisierte Merkmalsausprägung des Reizes geringer ist als die durch die realisierte Kategoriengrenze repräsentierte Merkmalsausprägung.

Simulation

Ausgangsdaten

        K1 K2 K3 K4 K5 K6 K7
Alkohol  0  0  7  6 10  1  5
Ecstasy  0  0  2  0  2  5 20
Hanf     0  4  9  2 10  4  0
Heroin   0  0  0  0  1  2 26
Kokain   0  0  1  0  2  7 19
Nikotin  0  0  4  7 15  2  1
Kaffee   4 14  9  1  1  0  0

Parameterschätzungen

$categories
        K1         K2         K3         K4         K5         K6 
-3.3433944 -2.7682074 -1.0656022 -0.7995195  0.3882297  1.1492867 

$objects
    Alkohol     Ecstasy        Hanf      Heroin      Kokain     Nikotin 
 0.01146844  0.92507345 -1.05873662  1.91960827  1.04959755 -0.11416839 
     Kaffee 
-2.73284269 

$objects.0
 Alkohol  Ecstasy     Hanf   Heroin   Kokain  Nikotin   Kaffee 
2.744311 3.657916 1.674106 4.652451 3.782440 2.618674 0.000000

Simulation von Daten auf Basis der Parameter

Simulierte Daten

        K1 K2 K3 K4 K5 K6 K7
Alkohol  0  0  0 11 60 27  2
Ecstasy  0  0  0  1 19 40 40
Hanf     0  2 44 31 23  0  0
Heroin   0  0  0  0  0 13 87
Kokain   0  0  0  0 12 38 50
Nikotin  0  0  2 22 52 23  1
Kaffee  12 40 48  0  0  0  0

Dichteverteilung der Ratings

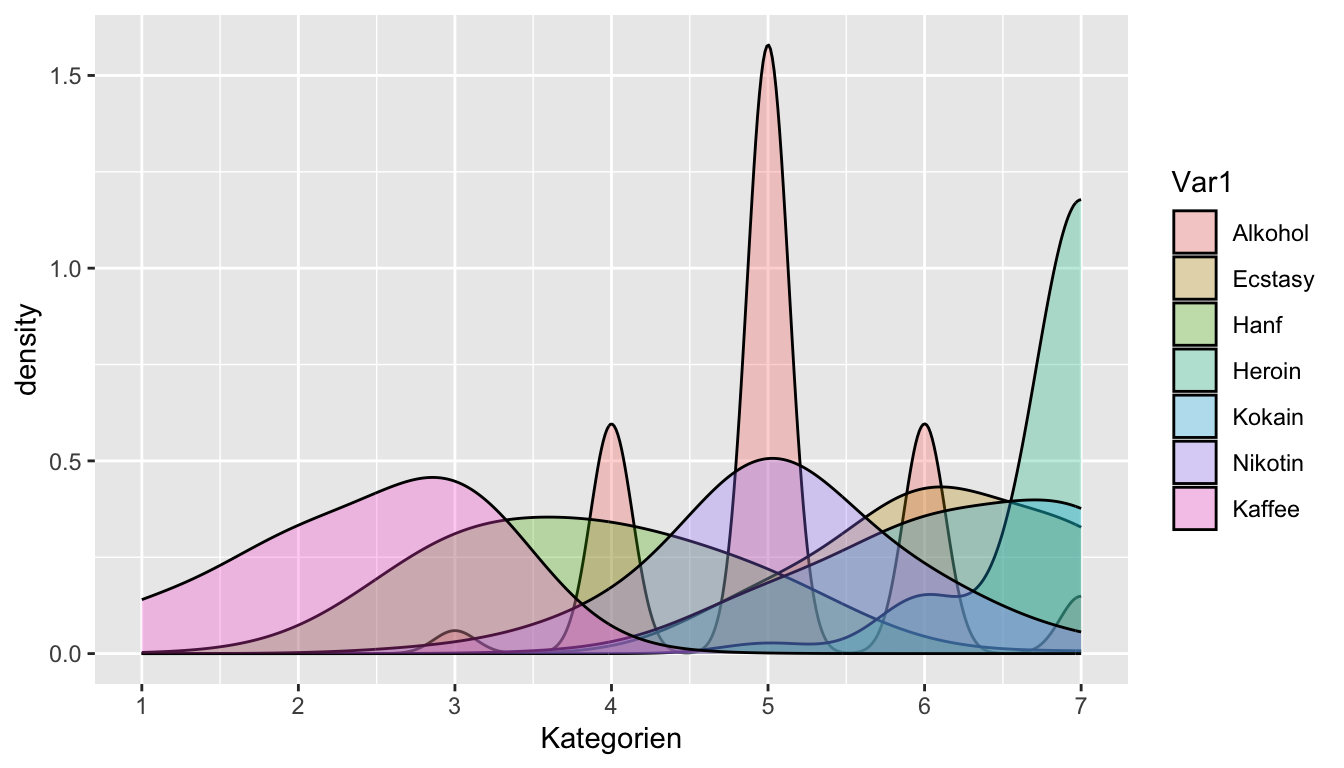
Schätzungen der Parameter

$categories
        K1         K2         K3         K4         K5         K6 
-3.3555837 -2.9426683 -1.9016046 -1.0341926  0.4231565  1.5635837 

$objects
    Alkohol     Ecstasy        Hanf      Heroin      Kokain     Nikotin 
 0.42152251  1.13739376 -1.59183160  2.07902744  1.46729064 -0.01364581 
     Kaffee 
-3.49975694 

$objects.0
 Alkohol  Ecstasy     Hanf   Heroin   Kokain  Nikotin   Kaffee 
3.921279 4.637151 1.907925 5.578784 4.967048 3.486111 0.000000

Test

Aus Gerich (). Thurstone- und Likertskalierung, 20XX).

Gefährlichkeitsbewertung verschiedener Substanzen auf einer Ratingskala von 1 bis 7 von 1=völlig ungefährlich, 7=sehr gefährlich).

        K1 K2 K3 K4 K5 K6 K7
Alkohol  0  0  7  6 10  1  5
Ecstasy  0  0  2  0  2  5 20
Hanf     0  4  9  2 10  4  0
Heroin   0  0  0  0  1  2 26
Kokain   0  0  1  0  2  7 19
Nikotin  0  0  4  7 15  2  1
Kaffee   4 14  9  1  1  0  0

Zeilenweise kumulierte relative Häufigkeiten

          K1   K2   K3   K4   K5   K6 K7
Alkohol 0.00 0.00 0.24 0.45 0.79 0.83  1
Ecstasy 0.00 0.00 0.07 0.07 0.14 0.31  1
Hanf    0.00 0.14 0.45 0.52 0.86 1.00  1
Heroin  0.00 0.00 0.00 0.00 0.03 0.10  1
Kokain  0.00 0.00 0.03 0.03 0.10 0.34  1
Nikotin 0.00 0.00 0.14 0.38 0.90 0.97  1
Kaffee  0.14 0.62 0.93 0.97 1.00 1.00  1

Zur Häufigkeit gehörige z-Werte. Die Verteilung der Ratings wird als NV um den wahren Wert angenommen. Die P-Werte 0 und 1 Werte haben als korrespondierende z-Werte -/+ Inf. Aus diesem Grund werden diese Werte hier mit 0.0001 bzw. .9999 substituiert, um nutzbare z-Werte zu erhalten. Die letzte Kategorie liefert keine zur Skalierung nutzbaren Informationen, da Sie für jede Kategorie $P = 1$ beträgt. Sie wird deshalb ausgelassen.

           K1    K2    K3    K4    K5    K6
Alkohol -3.72 -3.72 -0.70 -0.13  0.82  0.94
Ecstasy -3.72 -3.72 -1.48 -1.48 -1.09 -0.49
Hanf    -3.72 -1.09 -0.13  0.04  1.09  3.72
Heroin  -3.72 -3.72 -3.72 -3.72 -1.82 -1.26
Kokain  -3.72 -3.72 -1.82 -1.82 -1.26 -0.40
Nikotin -3.72 -3.72 -1.09 -0.31  1.26  1.82
Kaffee  -1.09  0.31  1.48  1.82  3.72  3.72

Die Lokation der Kategoriegrenzen ergibt sich durch die spaltenweise Mittelung der z-Werte.

   K1    K2    K3    K4    K5    K6 
-3.34 -2.77 -1.07 -0.80  0.39  1.15

Die Werte für die beurteilten Objekte ergeben sich als Zeilenmittel.

Alkohol Ecstasy    Hanf  Heroin  Kokain Nikotin  Kaffee 
  -1.08   -2.00   -0.01   -2.99   -2.12   -0.96    1.66

Als letzte Schritt wird von dem Mittel der Kategorielokationen die Objektlokationen abgezogen.

Alkohol Ecstasy    Hanf  Heroin  Kokain Nikotin  Kaffee 
   0.01    0.93   -1.06    1.92    1.05   -0.11   -2.73

Test

thurstone_msi(m.f)

$categories
        K1         K2         K3         K4         K5         K6 
-3.3433944 -2.7682074 -1.0656022 -0.7995195  0.3882297  1.1492867 

$objects
    Alkohol     Ecstasy        Hanf      Heroin      Kokain     Nikotin 
 0.01146844  0.92507345 -1.05873662  1.91960827  1.04959755 -0.11416839 
     Kaffee 
-2.73284269 

$objects.0
 Alkohol  Ecstasy     Hanf   Heroin   Kokain  Nikotin   Kaffee 
2.744311 3.657916 1.674106 4.652451 3.782440 2.618674 0.000000

Skalenwerte und Objektwerte auf dem Merkmalskontinuum

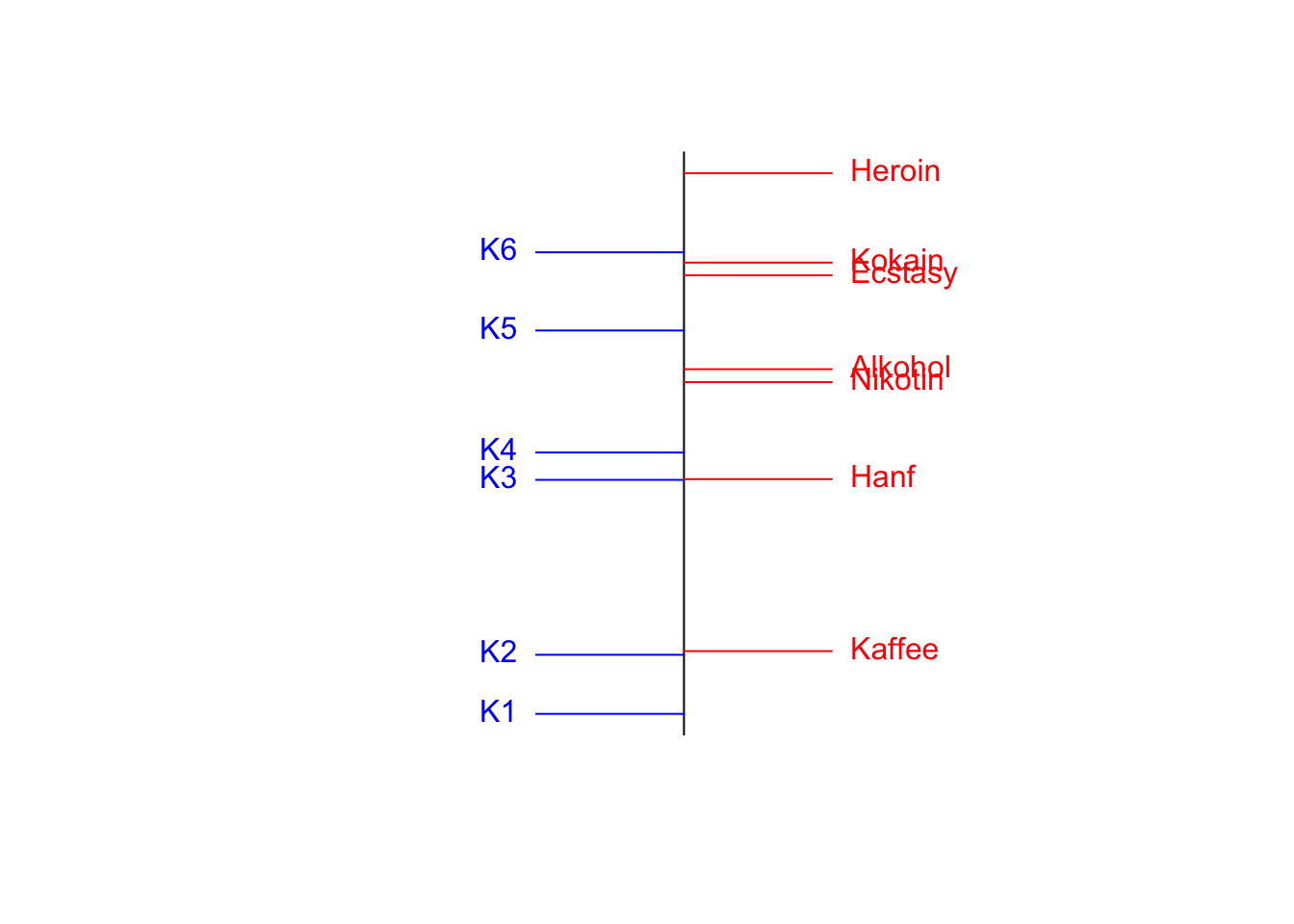
Beispiel II

Fünf Therapieprotokoll A-E sollen in Bezug auf das Merkmalskontinuum emotional Wärme skaliert werden. Hierzu liegen die Urteile von $n = 50$ Probanden auf einer Ordinalskala vor. Diese lautet wie folgt: 1= “sehr viel”, 2=“viel”, 3=“neutral”, 4=“wenig”, 5=“gar nicht”. Das Ergebnis ist folgende Kontingenztabelle.

     [,1] [,2] [,3] [,4] [,5]
[1,]    2    8   10   13   17
[2,]    5   10   15   18    2
[3,]   10   12   20    5    3
[4,]   15   20   10    3    2
[5,]   22   18    7    2    1

Berechnen wir die relativen Häufigkeiten.

     [,1] [,2] [,3] [,4] [,5]
[1,] 0.04 0.16 0.20 0.26 0.34
[2,] 0.10 0.20 0.30 0.36 0.04
[3,] 0.20 0.24 0.40 0.10 0.06
[4,] 0.30 0.40 0.20 0.06 0.04
[5,] 0.44 0.36 0.14 0.04 0.02

Kumulierte relative Häufigkeiten

     [,1] [,2] [,3] [,4] [,5]
[1,] 0.04 0.20 0.40 0.66    1
[2,] 0.10 0.30 0.60 0.96    1
[3,] 0.20 0.44 0.84 0.94    1
[4,] 0.30 0.70 0.90 0.96    1
[5,] 0.44 0.80 0.94 0.98    1

Thurstone macht die Annahme NV.

           [,1]       [,2]       [,3]      [,4]
[1,] -1.7506861 -0.8416212 -0.2533471 0.4124631
[2,] -1.2815516 -0.5244005  0.2533471 1.7506861
[3,] -0.8416212 -0.1509692  0.9944579 1.5547736
[4,] -0.5244005  0.5244005  1.2815516 1.7506861
[5,] -0.1509692  0.8416212  1.5547736 2.0537489

Spaltensummen und Sapltenmittel

Zeilensummen und Zeilenmittel

                                                       ZS          ZM
   -1.7506861 -0.84162123 -0.2533471 0.4124631 -2.4331913 -0.60829782
   -1.2815516 -0.52440051  0.2533471 1.7506861  0.1980811  0.04952027
   -0.8416212 -0.15096922  0.9944579 1.5547736  1.5566410  0.38916026
   -0.5244005  0.52440051  1.2815516 1.7506861  3.0322376  0.75805941
   -0.1509692  0.84162123  1.5547736 2.0537489  4.2991745  1.07479363
SS -4.5492286 -0.15096922  3.8307830 7.5223578  6.6529430  1.66323575
SM -0.9098457 -0.03019384  0.7661566 1.5044716  1.3305886  0.33264715

Durchschnitt Kategoriengrenze

[1] 0.3326472

                                                       ZS          ZM
   -1.7506861 -0.84162123 -0.2533471 0.4124631 -2.4331913 -0.60829782
   -1.2815516 -0.52440051  0.2533471 1.7506861  0.1980811  0.04952027
   -0.8416212 -0.15096922  0.9944579 1.5547736  1.5566410  0.38916026
   -0.5244005  0.52440051  1.2815516 1.7506861  3.0322376  0.75805941
   -0.1509692  0.84162123  1.5547736 2.0537489  4.2991745  1.07479363
SS -4.5492286 -0.15096922  3.8307830 7.5223578  6.6529430  1.66323575
SM -0.9098457 -0.03019384  0.7661566 1.5044716  1.3305886  0.33264715
            MA
   -0.94094497
   -0.28312688
    0.05651311
    0.42541226
    0.74214648
SS  1.33058860
SM  0.00000000

Lineare Transformation, um einen künstlichen Nullpunkt zu konstruieren.

MA

                                                                     SS 
-0.94094497 -0.28312688  0.05651311  0.42541226  0.74214648  1.33058860 
         SM 
 0.00000000

#MA <- MA + abs(min(MA))
#MA

Literatur

Gerich, J. (2010). Thurstone-und Likertskalierung. In C. Wolf & H. Best (Eds.), Handbuch der sozialwissenschaftlichen Datenanalyse (pp. 259–281). VS Verlag für Sozialwissenschaften.